Forma general
Una función cuadrática está expresada en forma general si está escrita como \(f(x)=ax^2+bx+c\), con \(a\), \(b\) y \(c\) números reales y \(a \neq 0\).
- Ejemplo: \[f(x) = x^2 - 10x + 24\]
Forma factorizada
Dada una función cuadrática expresada en forma general \(f(x)=ax^2+bx+c\), podemos escribirla como un producto utilizando sus raíces y su coeficiente principal.
Esta es conocida como la forma factorizada de la función cuadrática: \(f(x)=a(x−x_{1})(x−x_{2})\), donde \(x_{1}\) y \(x_{2}\) son las raíces de la función.
- Ejemplo: La forma factorizada de la función \(f(x) = x^2 - 10x + 24\) es \(f(x) = (x - 4)(x - 6)\)
Forma normal o estándar
Una función cuadrática escrita en forma general \(f(x)=ax^2+bx+c\), se puede transformar o expresar en su forma normal o estándar como \(f(x) = a(x – h)^2+ k\).
Para realizar este proceso, es necesario que \(b \neq 0\) (b sea distinto de cero). Posteriormente, con la técnica de completar el cuadrado, la función cuadrática en forma general se puede llegar a expresar como \(f(x) = a(x – h)^2 + k\), conocida como forma normal o estándar, para determinados números reales, h y k.
Esos números h y k se corresponden con el valor de la coordenada x y la coordenada y, respectivamente del vértice de la parábola \(V=(x_{v},y_{v})\).
Es decir: \((h , k) = (x_{v}, y_{v})\)
- Ejemplo: Para expresar de la forma general \(f(x) = x^2 - 10x + 24\) a la forma normal o estándar aplicaremos la técnica de completar el cuadrado. Basta observar en este caso que:
\(x^2 - 10x + 24 = (x^2 - 10x) + 24\)
\(x^2 - 10x + 24 = (x^2 - 2·5·x + 5^2 - 5^2) + 24 \)
\(x^2 - 10x + 24 = (x^2 - 2·5·x + 5^2) - 5^2 + 24 \)
\(x^2 - 10x + 24 = (x^2 - 2·5·x +5^2) - 25 + 24 \)
\(x^2 - 10x + 24 = (x - 5)^2 - 25 + 24\)
\(x^2 - 10x + 24 = (x - 5)^2 - 1\)
De esta manera, hemos transformado la función cuadrática escrita en forma general \(f(x) = x^2 - 10x + 24\) y la hemos expresado en la forma normal o estándar \(f(x) = (x - 5)^2 - 1\).
Representación gráfica
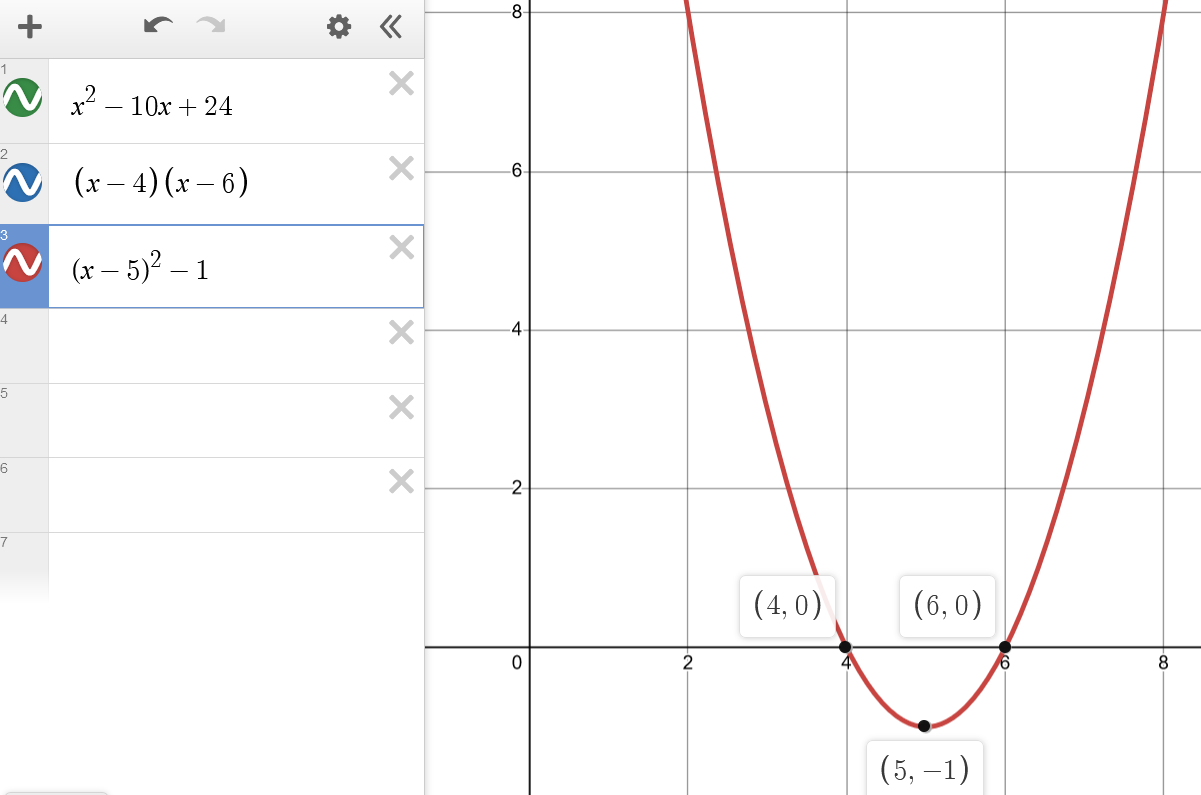
En esta imagen se puede observar como la representación gráfica de las tres expresiones se superponen.
|
Forma general |
\(f(x) = x^2 - 10x + 24\) |
|
Forma factorizada |
\(f(x) = (x - 4)(x - 6)\) |
|
Forma normal o estándar |
\(f(x) = (x - 5)^2 - 1\) |
Además, se puede observar claramente que las raíces de la función son x=4 y x=6 como se deduce de la forma factorizada y que el vértice de la parábola es el punto (5,-1), como se puede deducir de la forma estándar.